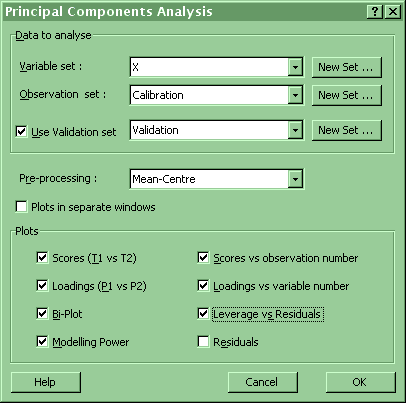
Principal Components Analysis PCA (Principal Components Analysis) is one of the most widely used multivariate techniques. For multivariate data, it helps visualisation by finding combinations of the original variables which best represent the variation in the data. Chemetrica provides a very flexible implementation of PCA and the dialogue box with the various options is shown below: Chemetrica has a wide range of options in its PCA routines: Analysis can be based on the covariance matrix (mean-centred values), the correlation matrix (autoscaled values) or a simple cross-product matrix (no scaling or centring) Malinowski model functions IND, RE, IE and F-tests for eigenvalues Scree plot output Hotelling T2 and Rao tests for outliers A separate validation set can be used to select the number of principal components in a model, with PRESS plot. Sample residuals and leverage for determining influential or badly-modeled observations Bi-Plots to relate variables and observations Modelling power, which shows which of the original variables are the most important for the principal components model Bi-Plots show both scores and loadings. The scores represent the observations, and the loadings represent the variables, so the bi-plot shows how variables and observations are related. PCA models work by only selecting the first few principal components. The sample residual shows how much error is introduced by only selecting some of the principal components. The leverage shows how much influence each observation has on the model. Combining these two measures shows observations where the model may be poor, which have the most influence on the model, and finally, observations with both high sample residual and high leverage may be outliers which have strongly distorted the model, and should be further examined. Return to the Chemetrica features page.